Find all occurrences of a finite set of strings in a given search string in linear time!
 on [Unsplash](https://unsplash.com?utm_source=medium&utm_medium=referral)](https://cdn-images-1.medium.com/max/10944/0*EQ2Vvn9Q1onWNiOM)
The Aho-Corasick algorithms allows you to find any amount of substrings and their position in a given search string. It does so in linear time. If the substrings are known beforehand, it is also possible to prepare them to later find matches in input strings faster.
Characteristics
Inputs are a finite set of search strings (the “dictionary”) and the input string in which those dictionary strings are searched for.
Output is a list of matched strings and their index in the input string. The list may include the same dictionary entries multiple times if they were found at multiple indices. The list is also sorted ascending by the index.
Runtime complexity is O(L₁ + L₂ + M) without preparation or O(L₁ + M) if you prepare the dictionary beforehand. L₁ is the length of the input string; L₂ is the sum of the lengths of all search strings; and M is the amount of matches that a search string will produce. Preparation has a runtime complexity of O(L₂).
Space complexity is O(L₂) in the worst case, but can be better if the dictionary strings share a lot of common prefixes.
The Aho-Corasick algorithm was developed by Alfred V. Aho and Margaret J. Corasick in their paper “Efficient string matching: An aid to bibliographic search”
Principle
The basic idea behind the Aho-Corasick is to first convert the dictionary into a trie, where each node represents a prefix of a dictionary entry (or the entry itself). A trie is a special form of tree where all nodes represent strings and the children of each node contain the parent’s string plus an additional character at the end. The root node is the empty string (here represented by ε). Let’s look at an example.
Basic Trie
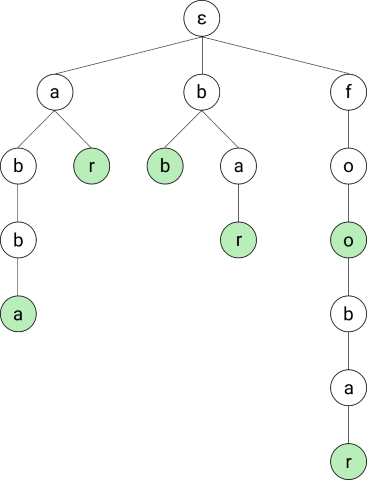 Image made by the author
Image made by the author
All examples in this blog post will use a dictionary with the following dictionary:
abba
bb
bar
ar
foobar
Those will result in the trie shown on the side (or top on mobile). The dictionary entry abba, for instance, was transformed into the four left-most nodes.
All nodes representing strings in the dictionary are also specifically marked so that we can recognize them when traversing over them. In the images, I marked them in green.
Using that trie we can now easily find out that the input string “bar” matches an entry in our dictionary by starting at the root and traversing over b to a to r.
Suffix Links
But looking at the input string “abar” we’d first traverse from a to b and then find out that we do not have a matching child. In that case we want to jump to the longest suffix of our current string (ab) that is in our tree: b. Note that the empty string is always the shortest suffix of every string. So if there is no longer substring in our tree, we’ll end up back at the root.
Since each node in the trie always has the same longest suffix, we can just remember those connections and include them in our initial tree creation. I’ve added those connections in the following image:
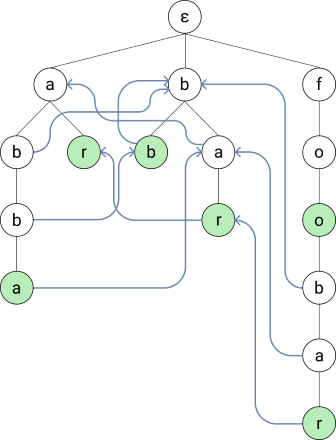 Image made by the author
Image made by the author
Dictionary Suffix Links
The last problem that we have now is that we might miss some entries in our dictionary. Let’s take for example the input string “foobar”. We’ll successfully find the words foo and foobar since we directly traverse of their nodes. But we won’t find the dictionary strings bar and ar without an additional (the last) trick.
We add another link from each node to the longest suffix that is in the dictionary — the so-called “dictionary suffix links”. Now, whenever we traverse a node, we simply follow the dictionary suffix links (the green arrows in the image) to find all dictionary strings for that node.
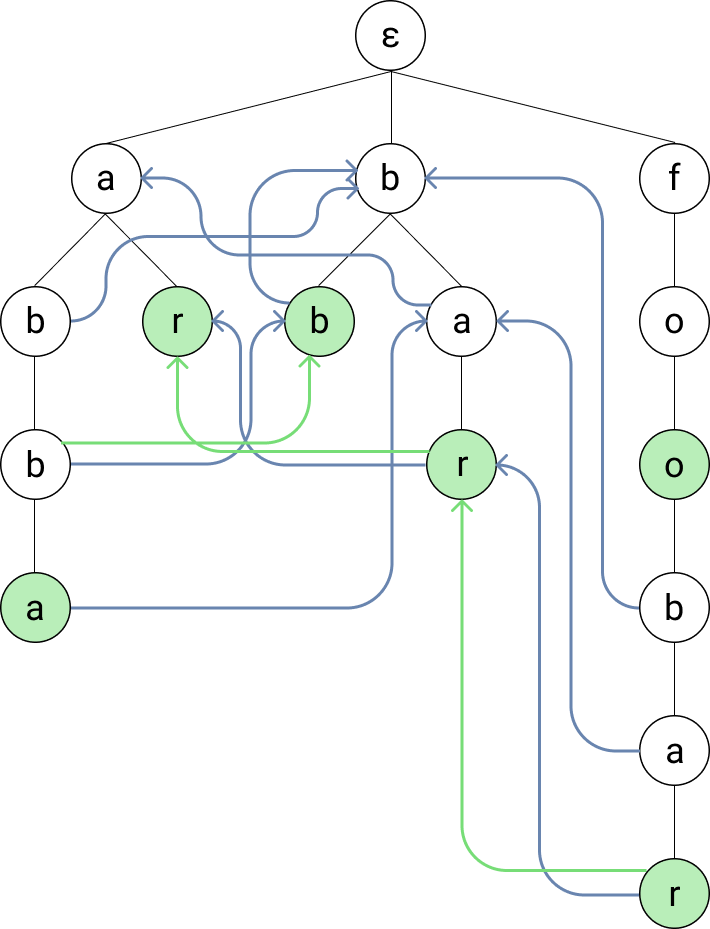 Image made by the author
Image made by the author
To summarize, each node now has three different kind of links to other nodes:
Any amount of child links
One suffix link to the node with the longest shared suffix
At most one dictionary suffix link to the node with the longest shared suffix that also represents a dictionary entry
An Example
Now let’s try with the input string “aabbTfoobar”. This will require the use of all three links.
Warning: the trie is going to look pretty full now with the path drawn on it. I go through it step-by-step, so bear with me. You can also just try to do it yourself first.
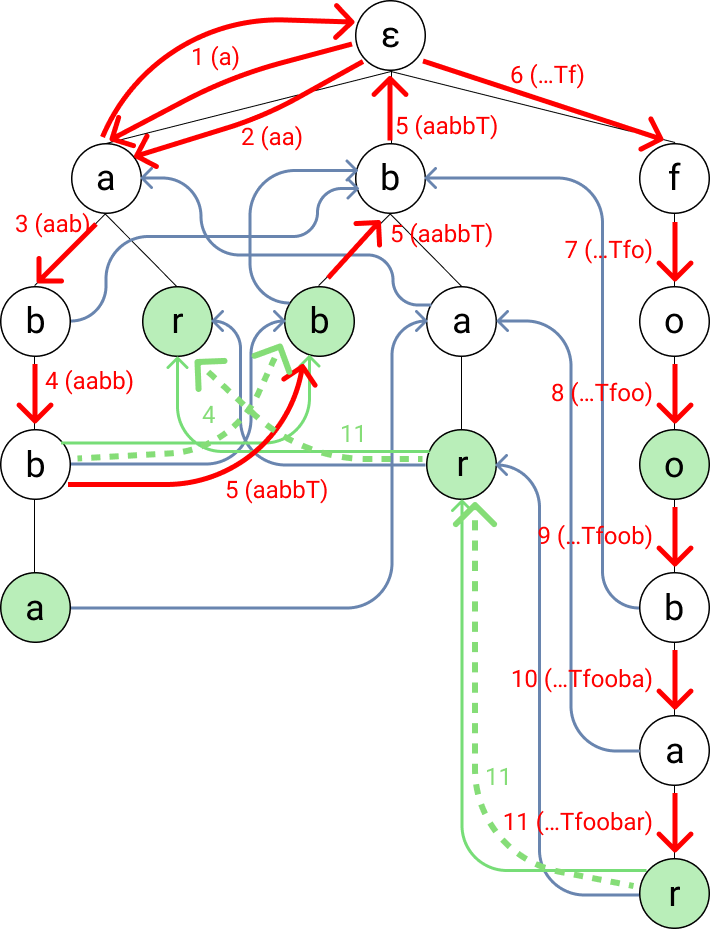 Image made by the author
Image made by the author
We start at ε and move to (a).
The node (a) doesn’t have a child with the string b, so we go back to the root and see if it has a matching child. It has. And we and up back at the same node.
We move to the child (ab).
We move to the child (abb). This node has a dictionary suffix link, so we follow it and find the dictionary entry bb.
The node doesn’t have a child for “T”, but it has a suffix link. So we follow that link to (bb). Since that node doesn’t have a fitting child either, we move to its suffix link (b). Again, no match and this time no suffix link, so we move to (ε). When (ε) has no fitting child, we just stay on it and still advance in the string.
We move to the child (f).
We move to the child (fo).
We move to the child (foo) and find the dictionary entry foo.
We move to the child (foob).
We move to the child (fooba).
We move to the child (fooobar) and find the dictionary entry foobar. Since the node also has a dictionary suffix link, we follow it and find the dictionary entry bar. Again, that node has a dictionary suffix link, so we find ar.
…and then we’re done. And we found all substrings in our dictionary.